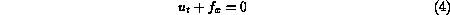


Following the presentation of Hirsch (1990) [11], we will distinguish two different levels at which the physical properties of the problem can be introduced in the discretization. At the first level, only information about the sign of the propagation speed of characteristic waves is taken into account. Let us consider, for sake of simplicity, a one-dimensional system of conservation laws in differential form:
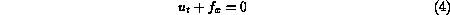
where  is a set of conserved quantities and
is a set of conserved quantities and 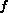 its
its 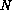 -component
flux vector. Then the first-order upwind scheme can be written as:
-component
flux vector. Then the first-order upwind scheme can be written as:
where 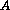 is the Jacobian matrix
is the Jacobian matrix
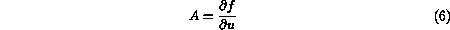
which is diagonalized by the matrix of left and right eigenvectors
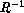 and
and 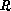
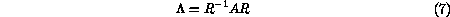
and 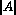 is defined as
is defined as
In the non-linear case,
for a general system of conservation laws, the Jacobian matrix 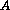 and
the matrix
and
the matrix 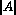 have non-constant terms, which can generally depend on
the solution. The usual approach to a numerical discretization consists
in locally freezing the coefficients of the matrices varying with the
solution, about an average estimate of the state variables.
The choices usually considered in literature are the arithmetic
average and the Roe's average. Different ways of taking in consideration
the eigenvalues of the Jacobian matrix and the propagating waves have
been widely explored in the last decade; we mention for completeness
the flux-vector splitting, where flux terms are split and
discretized directionally according to the sign of the associated
propagation speeds.
have non-constant terms, which can generally depend on
the solution. The usual approach to a numerical discretization consists
in locally freezing the coefficients of the matrices varying with the
solution, about an average estimate of the state variables.
The choices usually considered in literature are the arithmetic
average and the Roe's average. Different ways of taking in consideration
the eigenvalues of the Jacobian matrix and the propagating waves have
been widely explored in the last decade; we mention for completeness
the flux-vector splitting, where flux terms are split and
discretized directionally according to the sign of the associated
propagation speeds.