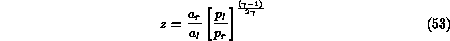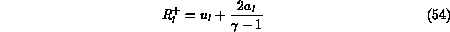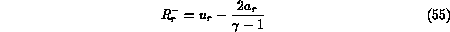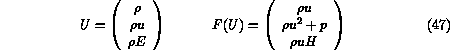


 appearing in the state equation and the ratio
of the specific heats
appearing in the state equation and the ratio
of the specific heats  .
Several different variables can be defined and several sets
can be used. The one-dimensional conservative set of variables
.
Several different variables can be defined and several sets
can be used. The one-dimensional conservative set of variables 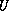 and its
physical flux function
and its
physical flux function 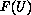 are
are
The physical state of the gas can be described by the previous set of
variables as well as by the primitive set 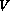 :
:
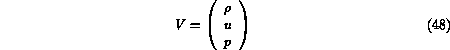
Let us define a temperature 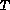 from the equation of state
from the equation of state 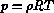 and the sound speed
and the sound speed  from the isentropic definition
from the isentropic definition
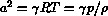 . The state of the gas can still
be defined by the set of variables
. The state of the gas can still
be defined by the set of variables 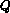 :
:
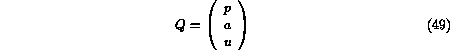
The initial discontinuity in Riemann problems for Euler equations will evolve in time breaking into leftward and rightward moving waves separated by a contact surface, see Anderson (1982) [12].
These propagating
waves can be either shocks or rarefaction waves depending on the initial
data. The available combinations can produce four different wave patterns
which are self-similar, i.e. they depend only on 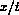 .
.
There is also a fifth pattern which is essentially of theoretical interest because it is the limit of the perfect gas equations at zero pressure and temperature and real-gas effects prevent its practical realization. This last case is defined by two rarefaction waves propagating rightward and leftward confined by two contact surfaces separated by a vacuum region in the middle.
A complete solution of the one-dimensional Riemann problem
requires the determination of the types of the waves, their relative
strenghts, and the flow properties in each region between the waves and
the contact surface. In the formulation of Gottlieb and Groth (1978)
[7],
the state of the gas is described by the set of variables 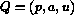 .
The unknowns are obtained solving the three conservation laws of
mass, momentum and energy and the equation of state, which reduces
to the well-known Rankine-Hugoniot relations across shocks and to
the well-known isentropic characteristic equations across rarefaction
waves. The flow-state is described by the initial left and right states
and by the six state variables
.
The unknowns are obtained solving the three conservation laws of
mass, momentum and energy and the equation of state, which reduces
to the well-known Rankine-Hugoniot relations across shocks and to
the well-known isentropic characteristic equations across rarefaction
waves. The flow-state is described by the initial left and right states
and by the six state variables 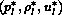 and
and
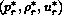 characterizing the solution
on the two sides of the contact surface. The known left state
characterizing the solution
on the two sides of the contact surface. The known left state
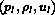 is connected to the unknown state
is connected to the unknown state
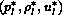 by the non-linear algebraic
relations describing the leftward moving wave. In the case of a
compression wave (or a shock), i.e.
by the non-linear algebraic
relations describing the leftward moving wave. In the case of a
compression wave (or a shock), i.e. 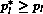 , the
shock-relations are employed; in the case of a rarefaction wave,
i.e.
, the
shock-relations are employed; in the case of a rarefaction wave,
i.e. 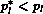 , rarefaction-waves relations are employed.
The right state
, rarefaction-waves relations are employed.
The right state 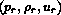 is similarly
connected to the unknown state
is similarly
connected to the unknown state 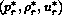 to the right of the contact surface. Finally, across the contact surface,
the following relations hold:
to the right of the contact surface. Finally, across the contact surface,
the following relations hold:
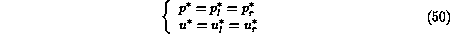
Appling this relations, the set of equations describing the Riemann
problem may be reduced to a single non-linear algebraic equation in one
unknown, the common flow velocity in the intermediate states 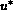 ,
for any particular wave pattern. This equation is generally
implicit in the unknown
,
for any particular wave pattern. This equation is generally
implicit in the unknown 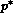 or
or 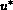 and an iterative solution
is provided by a standard Newton iterative method.
The initial guess
and an iterative solution
is provided by a standard Newton iterative method.
The initial guess 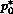 and
and  is provided by considering
compression waves instead of
shocks. This solution is exactly the same as for the pattern where
two isentropic rarefaction waves separated by a contact discontinuity
are present. The values of
is provided by considering
compression waves instead of
shocks. This solution is exactly the same as for the pattern where
two isentropic rarefaction waves separated by a contact discontinuity
are present. The values of 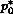 and
and 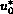 are given by
the following relations:
are given by
the following relations:
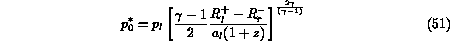
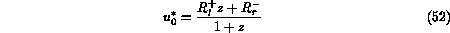
where  is a useful ratio of pressures and sound speeds and
is a useful ratio of pressures and sound speeds and
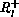
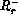 are the Riemann invariants for left- and right-ward
moving waves:
are the Riemann invariants for left- and right-ward
moving waves: